Appendix 4 - Numerical support for the tribal order and appointment

Having considered the proper derivation of the tribal CVs we now turn to examine briefly the significance of the order in which they are expressed in the WE matrix. With this in mind, a number of computer simulations have been undertaken which further establish the remarkable nature of the Encampment data.

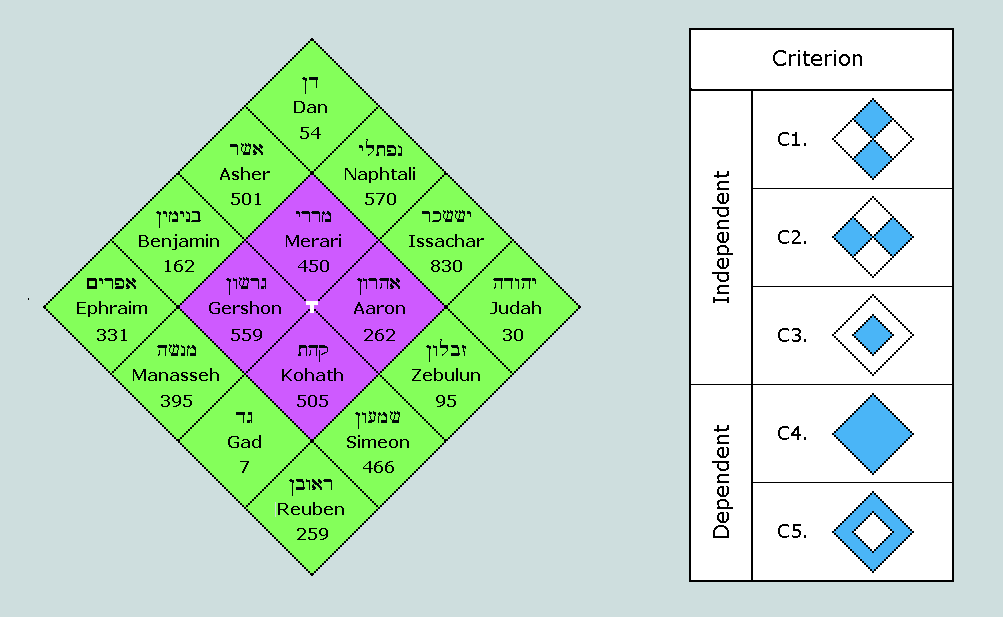
Clearly, 'order' has no influence on the principal matrix totals: 1776 (C3. - central block of four), 3700 (C5. - periphery of twelve) and 5476 (C4. - the whole). It is with the potentially-variable 'East-West' (C2.) and 'North-South' (C1.) divisions that we are concerned - those that, in the above 'canonical' case, provide the fruitful geometries that subdivide the square representing the whole matrix symmetrically. These are determined largely by order and value of each of the peripheral elements.

A Visual Basic program has been written to generate all 479,001,600 permutations* of these (C3. remaining fixed) - calculating C1. for each, and asking whether it has the canonical value, 2812 (= 4x703). [Observe that if this is the case, then C2. must, automatically, be its complement, 2664 (= 4x666]. Of this vast number of ways of arranging the tribes about the tabernacle, 518,400 are found to yield the desired result.

The chance of finding one of these patterns is therefore 1 in 479,001,600 / 518,400, or 1 in 924.

This suggests that some considerable thought was taken in deciding the observed order.

* Difficult to believe, perhaps, but consider: Beginning with the easternmost cell, any of the 12 names may occupy this position. Then, proceeding clockwise, any of the remaining 11 may occupy the second position; any of the remaining 10, the third position; and so on - the final 1 remaining, occupying the twelfth position. The total of possible unique patterns must therefore be 12x11x10x9x8x7x6x5x4x3x2x1, or 479,001,600.

VJ

2010-04-23