Appendix 1 - The unique numerical geometry of 37

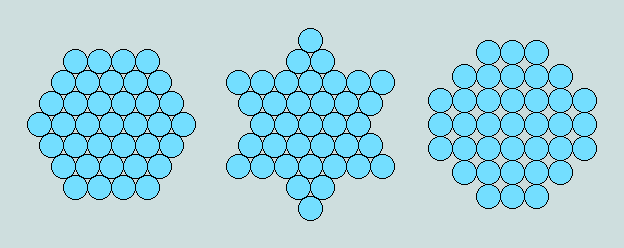
The geometrical attributes of certain whole numbers (when these are expressed as collections of uniform circular or spherical counters) represent eternal truths that may be readily grasped by all who have an eye for regularity of form and possess the ability to count - in short, that includes most of us! Such numbers are said to be figurate. About 5000 of these occur among the first million natural numbers; of these, some 60 or so may assume two distinct forms as, for example, 64 which is both square (8x8) and cube (4x4x4). Extending the range without limit, there are just two examples which transcend such figuracy and bifiguracy; they are the trifigurates 37 and 91. The first displays plane symmetries as hexagon, hexagram and octagon, while the latter has two plane symmetries, viz triangle and hexagon - and one solid, viz pyramid.

Present interest focuses on 37. Here are the geometrical details:

The two first realisations (hexagon and hexagram) each have 6 axes of symmetry; the last (octagon, or truncated square), 4.

For further information on the figurate numbers please click here.

Vernon Jenkins MSc

2001-11-18