Appendix 4 - Alternative vector multipliers

An Arithmetic Progression (AP) has the general form

a, a+d, a+2d, a+3d,... a+(n-1)d...

where a, d, and n represent, respectively, the first term, common difference, and position of the term in the progression. For our purposes here both a and d are positive or negative integers (ie whole numbers).

It is here demonstrated that all symmetrical vector multipliers of the form {A,B,C,D,C,B,A} will, when applied to the Genesis 1:1 set, produce a multiple of 37, provided {A,B,C,D} are the successive terms of some AP.

First, let us reduce the numerics of Genesis 1:1 to their modulo 37 form, thus:

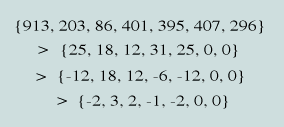
Now, writing the general up/down AP of 7 terms as

{a, a+d, a+2d, a+3d, a+2d, a+d, a}

and multiplying by {-2, 3, 2, -1, -2, 0, 0} we obtain

 

a(- 2 + 3 + 2 - 1 - 2 + 0 + 0) + d(3 + 4 - 3 - 4 + 0) = 0

In other words, the process must yield a multiple of 37 irrespective of the choice of a and d!

Vernon Jenkins MSc

2001-11-18