Link4.htm - The generation of symmetrical hexagon/hexagram pairs

In each of the following developments we shall assume our target to be the third such pair, viz 19/37.

Method 1: The self-intersection/self-union of any G-triangle (i.e. a numerical triangle set around a single central counter)

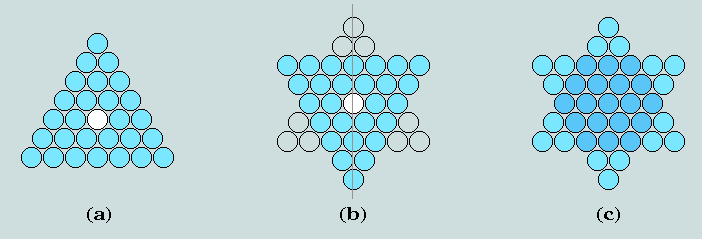
Here, at (a), we have 28-as-triangle - its centroid counter rendered white. At (b), a copy of this triangle is shown rotated through 180 degrees about its centroid, and at (c), the fusion of this copy with the original.

 

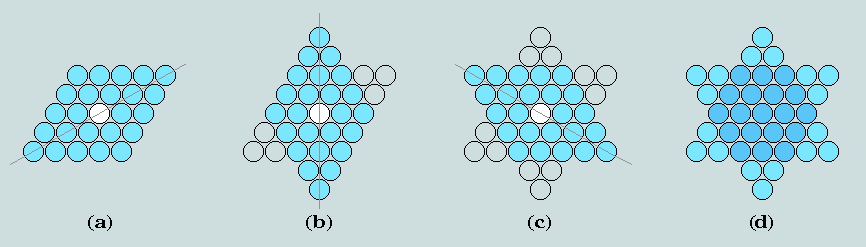
Method 2: The self-intersection/self-union of any odd rhombus (i.e. one possessing a single centroid counter)

At (a), we have 25-as-rhombus, at (b) a copy of the same rotated anticlockwise through 60 degrees and united with the original, at (c), a copy of the same rotated through a further 60 degrees, anticlockwise, and at (d) the fusion of these several figures.

 

Vernon Jenkins MSc

2007-07-07